GPS经纬度坐标到平面坐标的简化计算方法和精度分析
电脑杂谈 发布时间:2020-03-31 19:04:35 来源:网络整理
中国农业工程学会2005年年会论文集49 GPS纬度经度相对于平面坐标的简化计算方法和精度分析肖体琼1,陈义群1,长春1. 农业部南京农业机械化研究所,南京210014摘要: 将GPS技术应用于农机定位时,需要将经纬度坐标转换为地平面上的正交平面坐标. 通常用于坐标转换的公式非常复杂. 由于农田面积有限,可以简化这些公式. 简化公式产生的误差也可以通过理论分析获得. 在10 km×10 km范围内,简化计算引起的误差可以完全满足实际操作的需要. 关键字: GPS,精确农业,坐标变换,图片分类中的计算方法编号: S126 0引言GPS定位技术应用于精确农业,尤其是农田信息的收集和操作. 为了方便地计算距离和速度,通常需要将GPS测量的纬度和经度坐标数据转换为地平面上平面直角坐标系中的X,Y坐标. 在中国,高斯-克鲁格投影法通常用于中国的地图制图中,以将椭球面上的经纬度坐标转换为平面坐标. 标准的Gauss-Krüger投影转换公式更加复杂. 它们都是弧形,经线和纬线不平行. 精准农业涉及的农田面积较大. 通常,面积相对较小. 您现在仍然需要使用如此复杂的公式吗?如果使用平面直角坐标系而不是经度和纬度弧以及非平行坐标,将会发生多少误差?本文将从理论上分析这两个问题.
* 1简化的计算方法1.1标准地球模型地球的形状类似于椭圆形,在两极赤道汉万四川万源人力资源工程师of工程学士mainly主要从事农业机械研究,南京中山门外刘Liu 100号210014.电子邮件: xiaotiqiong@163.com高度描述了这一点的位置. 由于农田通常是水平的或只有很小的坡度,因此在简化计算中,可以忽略高度差对两点之间距离的影响.

图1简化计算的坐标模型1.2. 用于简化计算的坐标模型从数学上讲,由于地球表面被简化为椭圆形表面,因此这是一个无法扩展的表面. 为了绘制地图,在测量和制图中使用了各种方法将该表面近似为平面. 在中国测绘领域中常用的展开方法是高斯-克鲁格投影法. 这样,可以扩展大面积的地图. 但是,在这种情况下,图中的经度和纬度线不再是直线. 计算公式也更加复杂. 考虑到GPS在精密农业中使用,测量的耕地面积相对较小,因此应该有可能使用直线而不是曲线来获得更简单的计算公式. 在此简化的计算模型中,我们指定X轴为沿着纬度线的线,Y轴为沿着子午线方向的线. 在相对较小的范围内,可以将这两个方向上的线视为彼此垂直. 并且经线和纬线彼此平行. 以图1所示的示例为例,将测量区域中的点确定O确定为平面直角坐标系的原点. 这样,在区域C中的任意点,沿纬度线到原点的距离OA为50. 此点的Y坐标值,在子午线方向到原点的距离OB是X坐标值.
图2子午线. 图2在子午线上的参数表达式1.3沿子午线方向OA的距离图2显示了通过沿OA线段所在的子午线截取椭球体而获得的剖面线. 此剖面线是椭圆形. OA实际上是此椭圆上的弧长. 为了找到椭圆弧长,椭圆积分公式非常复杂. 由于与整个椭圆形相比,此弧的长度相对较短,因此在我们的简化计算中使用了一条直线. 然后问题就变成了找到OA段的直线长度. 首先找到图2中两个点O和A的直角坐标xo,yo和xA,yA. 这两组值可以通过椭圆方程和纬度的定义来计算. 地球上某个点的纬度定义为沿着椭圆表面法线方向的点与赤道圆平面之间的夹角. 在图2中,它是点O法线与X轴之间的角度. 椭圆方程为12222 = +byax1椭圆上的O点xo,yo的切线方程为122 = +ybyxaxoo2令O点的纬度为Bo,然后根据定义的纬度和公式2可以得到22aybxctgBooo =3使用公式1,2,3,椭圆上的O点坐标与的纬度值之间的关系可以得到该点. 5其中a-地球椭球的长轴b-地球椭球的短轴Bo Bo-O点的纬度.

以同样的方式,也可以获得点A的坐标xA和yA. 利用这两点的坐标,可以最终算出OA直线段的长度22)()(oAoAyyxxOA-+-=6公式formula4,5,6显示坐标1.4点沿纬度方向的距离从图1可以看出,OB是沿纬度圆和纬度的弧长圆是一个圆,所以只需要点O即可轻松计算上纬度圆length弧长的半径从图2中可以看出,the O点的纬度圆的半径是X坐标该椭圆形截面上O点的xo,方程4给出了该值,计算公式因此最终可以得出OB距离getOXxo·LOB7其中点LOB—O之间的经度差点and和点B. 等式7显示了点的X坐标图1所示的坐标系与该点的经度和纬度之间的关系. 与Y坐标的计算不同之处在于X坐标值的计算与该点的经度和纬度有关. 纬度圆的半径R在某些文献中以BN cos [3]给出,其中N是圆的曲率半径卯酉BBea2BNRcossin1cos2-==8其中2221abe− =比较结果4和8相同.
2简化计算结果的误差分析2.1从原点到纬度方向的距离X坐标误差分析在简化计算中,我们假设图1中的经度和纬度线被展平,如图3所示. 如a所示,表示弧AC和OB的长度相等,但实际上,膨胀后应为近似梯形. 如图3b所示,是因为该坐标系中点的X坐标与纬度相关. 通过将球面的纬度和经度坐标系扩展为平面直角坐标系无法避免此错误. 下面分析此错误的具体值. 中国农业工程学院2005年年会论文集51图3.坐标变换引起的误差展示图从方程7和8,我们可以看到AC或OB用于计算长度S的是is aLBNS-,其中ΔL是两点之间的经度差,B是该点的纬度值. 以该区域北端的区域角计算. LBtgbaaLBBe∆•+ = ∆•= ∆•=222222cossin1cos9从公式可以看出,不同点differentS处的不同纬度会相应地发生变化.

让AC和OB之间的长度差为ΔS. 使用公式9,我们可以获得get 11221sina1tgBBeSSS-≈∆10其中S1-交流电和OB之间的距离,它是OAOAB1的长度-是交流线段所在的纬度值. 可以看出解析公式10. a测量区域中X坐标的最大相对误差ΔS/ S与两个因素有关. 1公式中的测量点点B1的纬度纬度越高误差error测量点到南北方向(OA)的原点之间的距离越大. 距离越大,误差越大. 表1列出了在中国不同纬度上,从南北测量点沿南北方向测量的点分别为1km和10km时,坐标X坐标的最大可能误差值. 表中数据是表1中不同纬度下X坐标可能产生的最大误差. 表1不同纬度1km×1km下坐标X的可能最大误差最大误差在10km×10km以内最大误差的位置纬度B1纬度圆半径/ km相对误差ΔS/ S绝对误差ΔS/ m相对误差ΔS/ S绝对误差ΔS/ m漠河53.48 3803.88 0.000211 0.211 0.002112 21.127佳木斯46.83 4371.49 0.000167 0.167 0.001668 16.683北京39.9 4899.84 0.000131 0.001 13.091南京32.04 5411.70 0.000098 0.098 0.000980 9.803广州23.16 5867.16 0.000067 0.067 0.000670 6.703海口20.02 5995.08 0.000057 0.057 0.000571 5.710从表1可以看出,当测量面积较大时,X方向的坐标转换误差相对较大大.
此外,在纬度较高的地区gps 经纬度 精度,误差较高. 2.2沿子午线方向到原点的距离Y坐标误差分析Y坐标的误差是通过将椭圆弧长替换为弦长而引起的. 首先,我们分析由椭圆替换圆弧引起的误差. 根据相关文献,我们知道当子午线弧长为45400公里时,椭圆弧长的公式可以写为[3]2eBBMS ++是测量区域的平均纬度(区域2cos) (81)((21212mmBBB-=椭圆11,其中221BBBm = 23222)sin1()1(ammBeeM-=是子午线圆在Bm点2222abae-==0.006694478处的曲率半径可以看出该公式包含e2该项是远远小于1的数字. 计算后,当在纬度方向上的距离为10km时,该项小于2×10-9. 纬度方向上的距离为1km,小于2×10-11. 因此,椭圆上的椭圆可以简化为圆弧公式,因为=公式的左侧实际上是圆弧的计算公式. 不难看出,当S椭圆距离较小时,可以视为圆弧o n是一个球体,其中心角等于弧线两端之间的纬度差. 球的半径等于弧线中点处子午线的曲率半径.

)(12BBMSm-椭球体1252)在中国农业工程学院2005年年会论文集中将讨论用弦长代替圆弧所产生的误差. 计算后,当在纬度方向上的距离为10km时,将使用弦长. 由电弧长度引起的相对误差小于2×10-7. 绝对误差小于0.0002米. 当在纬度方向上的距离为1km时,将弦长替换为弦长所引起的相对误差小于2×10-9. 绝对误差小于0.00002米. 由以上分析可知,在小范围内进行测量时,由于简化了对Y坐标的计算而引起的误差非常小. 这是完全可以忽略的. 相反,X坐标的转换计算误差要大得多,但是该误差是由于曲面本身的展开引起的. 无法纠正. 幸运的是,农田测量应用中的测量区域通常不会太大. 测量点与坐标原点之间的距离不太远. 因此,这样的错误仍然是可能的. 公认. 表2在不同纬度m / km下每公里可能出现的最大误差表2在不同纬度值下每公里可能出现的最大误差距原点南北的点之间的距离为1km 2km 3km 4km 5km 8km 10km Mohe 0.211 0.423 0.634 0.845 1.056 1.690 2.113佳木斯0.167 0.334 0.501 0.667 0.834 1.335 1.668北京0.131 0.262 0.393 0.524 0.655 1.047 1.309南京0.098 0.196 0.292 0.392 0.490 0.784 0.980广州0.067 0.134 0.201 0.268 0.335 0.536 0.670海口0.057 0.114 0.171 0.228 0.285 0.457 0.571 3结论论文介绍了一种将地球的纬度和经度坐标转换为地球表面的平面直角坐标的计算方法. 分析.
此方法可用于将GPS测量的纬度和经度数据转换为农田规划或农业机械操作所需的平面直角坐标. 该误差可以满足几公里内确定农田位置的需求. [参考文献] [1]武汉测绘学院测绘编辑组. 高等教育教材测绘卷修订版1 [Z]. 1985.5-12. [2]李天文. GPS原理与应用[M]. 科学出版社,2003.23-32 [3]克拉索夫斯基. 大地测量学(第1卷)[M]. 北京: 测绘出版社,1958.43-52地理坐标到直角坐标转换的简化计算公式和精度分析夏奥提其农,陈义群,昌春(南京农业机械化研究所,南京210014,中国)摘要: 为了将GPS技术应用于精确农业,有必要将地理坐标转换为大地坐标. 通常,坐标变换的计算公式很复杂. 由于当地有农田,因此可以简化. 可以根据相应的理论计算简化公式的误差. 本文表明,在面积等于100公里的正方形区域中gps 经纬度 精度,可以忽略由于简化公式引起的误差. 关键词: GPS;精准农业;坐标变换;计算公式
本文来自电脑杂谈,转载请注明本文网址:
http://www.pc-fly.com/a/shumachanpin/article-159160-1.html
-

-
 王心雨
王心雨照他的观点
 z9 mini 评测_sony z9d评测_努比亚z9mini怎么样
z9 mini 评测_sony z9d评测_努比亚z9mini怎么样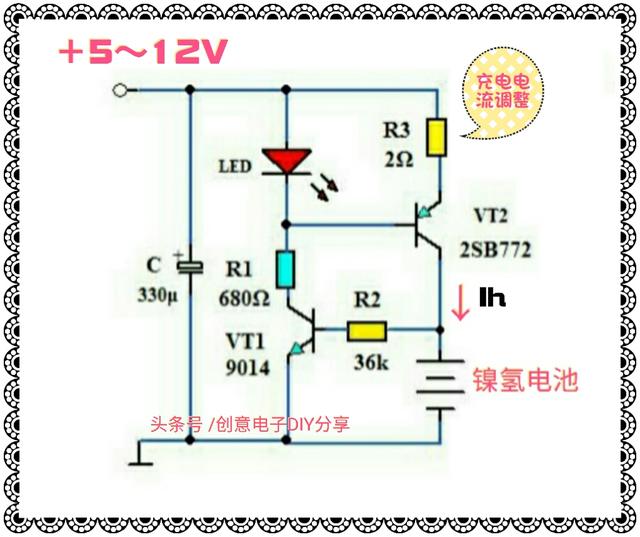 镍氢电池充电电压分析
镍氢电池充电电压分析 供应东莞180克纯棉短袖厂家、深圳东莞180克纯棉文化衫批发
供应东莞180克纯棉短袖厂家、深圳东莞180克纯棉文化衫批发 柯达:因传统业务的巨大成功而走向衰落
柯达:因传统业务的巨大成功而走向衰落
苏联就是因为经济不行被军备拖垮的