二分搜索树的前身和后继

您必须全面了解二叉树，那么二叉搜索树是什么？首先给出每个节点的属性: 1）关键字关键字2）p父节点3）左左子代4）右右子代定义如下: 对于任何节点x，左子树的关键字不超过x .key ，右子树的键必须至少为x.key. 以下所有属性都是围绕此定义开发的. 方法: 1）遍历搜索二叉树: 与遍历普通二叉树相同，按照中间和背面的顺序，这取决于您的选择. 时间复杂度为O（n）. n是节点数. 2）搜索二叉树: 由于二叉树的定义规则，搜索就像二分法，并且时间复杂度为O（h）. h是树的高度3）搜索树的最大和最小关键字: 类似于搜索二叉树，根据定义的规则，时间复杂度为O（h）4）插入和删除的时间复杂度为也是O（h）. 插入相对简单. 这与搜索二叉树直到该节点为空相同，然后该节点的位置就是插入位置. 删除要复杂一些，需要考虑三种情况. 我的重点是前任和后继.

前辈和前辈

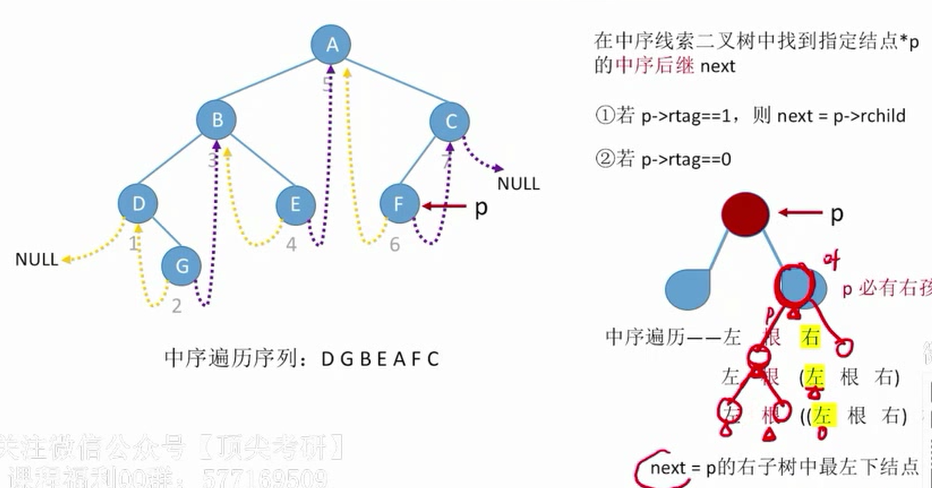
什么是后继者和前任者，如果对数节点的键顺序为: key1 <= key2 <= ...... <= keyn3 <= keyn2 <= keyn1 <= keyn，则keyn3和keyn1为keyn2. 寻找节点的后继者的前任者和后继者分为两种情况，即: 1）节点的右子树不为空； 2）将节点的右子树更改为空. 下面说明这两种情况. 1）右子树R不为空. 在这种情况下，找到继任者相对简单. 知道了搜索二叉树的定义后，如果我们通过Zhong Xu遍历二叉树，则输出关键字将按从小到大的顺序排序. 也就是说二叉树前驱后继，在遍历该节点之后，应遍历该节点的右子树，并且右子树不为空，指示该节点的后继必须在右子树中，并且具有最小键的节点在右子树中. 子树具有最小的键可以通过方法3）计算. 2）右子树R为空. 问题在于访问节点a之后，我们接下来应该访问哪个节点？首先要确定的是，接下来要访问的节点是根节点. 为什么？因为我们必须承认，除了根节点之外，任何节点都是节点子树的一部分. 对于右子树为空的情况二叉树前驱后继，在访问节点a之后，访问以该节点为根节点的树Z. 接下来，可以在两种情况下进行分析. 树Z是上一个节点的左子树. 显然，在访问了左子树Z之后，是时候访问子树的根节点e了. 然后，根节点是节点a的后继节点. 如果该子树是前一个节点的右子树Z，则意味着在访问根节点e之后访问了右子树. 因此，它的后继节点应该仍然位于较高的节点上，直到遇到该节点所在的子树是某个节点q的左子树的一部分为止. 节点q是此节点的后继节点. 前体前体和后继体是对称的，在此不再赘述. 1）如果节点的左子树不为空，则该节点的前任节点为左子树的最右节点（最大节点）2）如果该节点的左子树为空，则该节点继续返回其子树父节点，知道某个节点是其父节点的正确节点，那么父节点就是后继节点

本文来自电脑杂谈，转载请注明本文网址：
http://www.pc-fly.com/a/jisuanjixue/article-266848-1.html